Model stacking for boosted trees • stackgbm

Introduction

Model stacking (Wolpert 1992) is a method for ensemble learning that combines the strength of multiple base learners to drive up predictive performance. It is a particularly popular and effective strategy used in machine learning competitions.

stackgbm implements a two-layer stacking model: the first layer generates “features” produced by gradient boosting trees. The boosted tree models are built by xgboost (Chen and Guestrin 2016), lightgbm (Ke et al. 2017), and catboost (Prokhorenkova et al. 2018). The second layer is a logistic regression that uses these features as inputs.

library("stackgbm")

Generate data

Let’s generate some data for demonstrate purposes. The simulated data has a \(1000 \times 50\) predictor matrix with a binary outcome vector. 800 samples will be in the training set and the rest 200 will be in the (independent) test set. 25 out of the 50 features will be informative and follows \(N(0, 10)\).

sim_data <- msaenet::msaenet.sim.binomial(
  n = 5000,
  p = 100,
  rho = 0.8,
  coef = c(
    rnorm(20, mean = 0, sd = 5),
    rnorm(20, mean = 0, sd = 2),
    rnorm(20, mean = 0, sd = 1)
  ),
  snr = 0.5,
  p.train = 0.8,
  seed = 42
)

x_train <- sim_data$x.tr
x_test <- sim_data$x.te
y_train <- as.vector(sim_data$y.tr)
y_test <- as.vector(sim_data$y.te)

Parameter tuning

cv_xgboost(), cv_lightgbm() and cv_catboost() provide wrappers for tuning the most essential hyperparameters for each type of boosted tree models with k-fold cross-validation. The “optimal” parameters will be used to fit the stacking model later.

params_xgboost <- cv_xgboost(x_train, y_train)
params_lightgbm <- cv_lightgbm(x_train, y_train)
params_catboost <- cv_catboost(x_train, y_train)

Train the stackgbm model

model_stackgbm <- stackgbm(
  sim_data$x.tr,
  sim_data$y.tr,
  params = list(
    params_xgboost,
    params_lightgbm,
    params_catboost
  )
)

Inference

roc_stackgbm_train <- pROC::roc(
  y_train,
  predict(model_stackgbm, x_train)$prob,
  quiet = TRUE
)
roc_stackgbm_test <- pROC::roc(
  y_test,
  predict(model_stackgbm, x_test)$prob,
  quiet = TRUE
)
roc_stackgbm_train$auc
#> Area under the curve: 0.874
roc_stackgbm_test$auc
#> Area under the curve: 0.7016

Performance evaluation

Let’s compare the predictive performance between the stacking model and the three types of tree boosting models (base learners) fitted individually. Note that the models and performance metrics should be (bitwise) reproducible on the same operating system but they might vary on different platforms.

model_xgboost <- xgboost_train(
  params = list(
    objective = "binary:logistic",
    eval_metric = "auc",
    max_depth = params_xgboost$max_depth,
    eta = params_xgboost$eta
  ),
  data = xgboost_dmatrix(x_train, label = y_train),
  nrounds = params_xgboost$nrounds
)

model_lightgbm <- lightgbm_train(
  data = x_train,
  label = y_train,
  params = list(
    objective = "binary",
    learning_rate = params_lightgbm$learning_rate,
    num_iterations = params_lightgbm$num_iterations,
    max_depth = params_lightgbm$max_depth,
    num_leaves = 2^params_lightgbm$max_depth - 1
  ),
  verbose = -1
)

model_catboost <- catboost_train(
  catboost_load_pool(data = x_train, label = y_train),
  NULL,
  params = list(
    loss_function = "Logloss",
    iterations = params_catboost$iterations,
    depth = params_catboost$depth,
    logging_level = "Silent"
  )
)

xgboost

roc_xgboost_train <- pROC::roc(
  y_train,
  predict(model_xgboost, x_train),
  quiet = TRUE
)
roc_xgboost_test <- pROC::roc(
  y_test,
  predict(model_xgboost, x_test),
  quiet = TRUE
)
roc_xgboost_train$auc
#> Area under the curve: 0.8891
roc_xgboost_test$auc
#> Area under the curve: 0.6934

lightgbm

roc_lightgbm_train <- pROC::roc(
  y_train,
  predict(model_lightgbm, x_train),
  quiet = TRUE
)
roc_lightgbm_test <- pROC::roc(
  y_test,
  predict(model_lightgbm, x_test),
  quiet = TRUE
)
roc_lightgbm_train$auc
#> Area under the curve: 0.8768
roc_lightgbm_test$auc
#> Area under the curve: 0.6915

catboost

roc_catboost_train <- pROC::roc(
  y_train,
  catboost_predict(
    model_catboost,
    catboost_load_pool(data = x_train, label = NULL)
  ),
  quiet = TRUE
)
roc_catboost_test <- pROC::roc(
  y_test,
  catboost_predict(
    model_catboost,
    catboost_load_pool(data = x_test, label = NULL)
  ),
  quiet = TRUE
)
roc_catboost_train$auc
#> Area under the curve: 0.8697
roc_catboost_test$auc
#> Area under the curve: 0.7017

Tabular summary

We can summarize the AUC values in a table.

AUC values from four models on training and testing set
	stackgbm	xgboost	lightgbm	catboost
Training	0.8740	0.8891	0.8768	0.8697
Testing	0.7016	0.6934	0.6915	0.7017

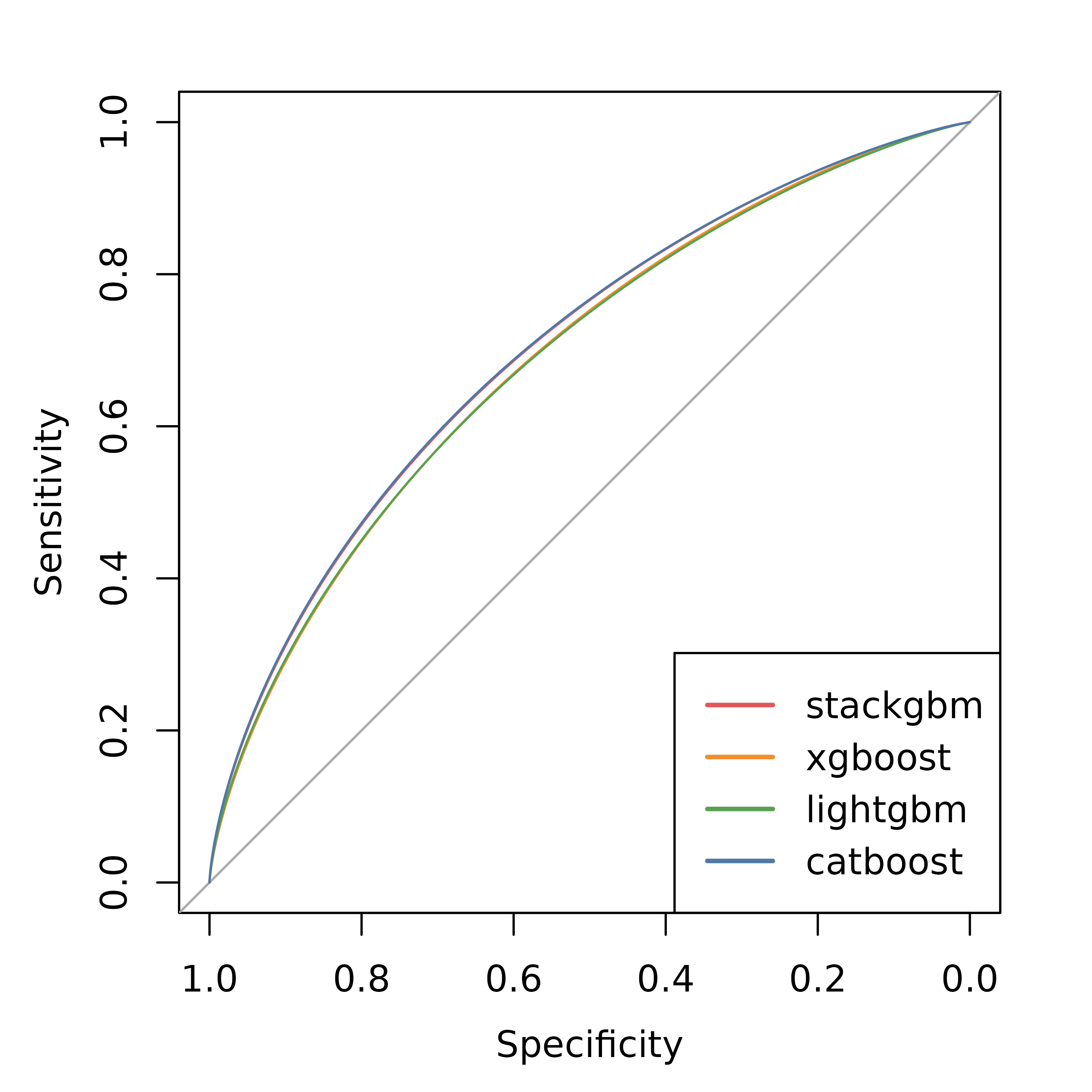
ROC curves

Plot the ROC curves of all models on the independent test set.

pal <- c("#e15759", "#f28e2c", "#59a14f", "#4e79a7", "#76b7b2")

plot(pROC::smooth(roc_stackgbm_test), col = pal[1], lwd = 1)
plot(pROC::smooth(roc_xgboost_test), col = pal[2], lwd = 1, add = TRUE)
plot(pROC::smooth(roc_lightgbm_test), col = pal[3], lwd = 1, add = TRUE)
plot(pROC::smooth(roc_catboost_test), col = pal[4], lwd = 1, add = TRUE)
legend(
  "bottomright",
  col = pal,
  lwd = 2,
  legend = c("stackgbm", "xgboost", "lightgbm", "catboost")
)

Notes on categorical features

xgboost and lightgbm both prefer the categorical features to be encoded as integers. For catboost, the categorical features can be encoded as character factors.

To avoid possible confusions, if your data has any categorical features, we recommend converting them to integers or use one-hot encoding, and use a numerical matrix as the input.

References

Chen, Tianqi, and Carlos Guestrin. 2016. “XGBoost: A Scalable Tree Boosting System.” In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–94. ACM.

Ke, Guolin, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie-Yan Liu. 2017. “LightGBM: A Highly Efficient Gradient Boosting Decision Tree.” In Advances in Neural Information Processing Systems, 3146–54.

Prokhorenkova, Liudmila, Gleb Gusev, Aleksandr Vorobev, Anna Veronika Dorogush, and Andrey Gulin. 2018. “CatBoost: Unbiased Boosting with Categorical Features.” In Advances in Neural Information Processing Systems, 6638–48.

Wolpert, David H. 1992. “Stacked Generalization.” Neural Networks 5 (2): 241–59.