Validate high-dimensional Cox models with time-dependent AUC

Validate high-dimensional Cox models with time-dependent AUC

Usage

validate(
  x,
  time,
  event,
  model.type = c("lasso", "alasso", "flasso", "enet", "aenet", "mcp", "mnet", "scad",
    "snet"),
  alpha,
  lambda,
  pen.factor = NULL,
  gamma,
  lambda1,
  lambda2,
  method = c("bootstrap", "cv", "repeated.cv"),
  boot.times = NULL,
  nfolds = NULL,
  rep.times = NULL,
  tauc.type = c("CD", "SZ", "UNO"),
  tauc.time,
  seed = 1001,
  trace = TRUE
)

Arguments

x

Matrix of training data used for fitting the model; on which to run the validation.

time

Survival time. Must be of the same length with the number of rows as x.

event

Status indicator, normally 0 = alive, 1 = dead. Must be of the same length with the number of rows as x.

model.type

Model type to validate. Could be one of "lasso", "alasso", "flasso", "enet", "aenet", "mcp", "mnet", "scad", or "snet".

alpha

Value of the elastic-net mixing parameter alpha for enet, aenet, mnet, and snet models. For lasso, alasso, mcp, and scad models, please set alpha = 1. alpha=1: lasso (l1) penalty; alpha=0: ridge (l2) penalty. Note that for mnet and snet models, alpha can be set to very close to 0 but not 0 exactly.

lambda

Value of the penalty parameter lambda to use in the model fits on the resampled data. From the fitted Cox model.

pen.factor

Penalty factors to apply to each coefficient. From the fitted adaptive lasso or adaptive elastic-net model.

gamma

Value of the model parameter gamma for MCP/SCAD/Mnet/Snet models.

lambda1

Value of the penalty parameter lambda1 for fused lasso model.

lambda2

Value of the penalty parameter lambda2 for fused lasso model.

method

Validation method. Could be "bootstrap", "cv", or "repeated.cv".

boot.times

Number of repetitions for bootstrap.

nfolds

Number of folds for cross-validation and repeated cross-validation.

rep.times

Number of repeated times for repeated cross-validation.

tauc.type

Type of time-dependent AUC. Including "CD" proposed by Chambless and Diao (2006)., "SZ" proposed by Song and Zhou (2008)., "UNO" proposed by Uno et al. (2007).

tauc.time

Numeric vector. Time points at which to evaluate the time-dependent AUC.

seed

A random seed for resampling.

trace

Logical. Output the validation progress or not. Default is TRUE.

References

Chambless, L. E. and G. Diao (2006). Estimation of time-dependent area under the ROC curve for long-term risk prediction. Statistics in Medicine 25, 3474–3486.

Song, X. and X.-H. Zhou (2008). A semiparametric approach for the covariate specific ROC curve with survival outcome. Statistica Sinica 18, 947–965.

Uno, H., T. Cai, L. Tian, and L. J. Wei (2007). Evaluating prediction rules for t-year survivors with censored regression models. Journal of the American Statistical Association 102, 527–537.

Examples

data(smart)
x <- as.matrix(smart[, -c(1, 2)])[1:500, ]
time <- smart$TEVENT[1:500]
event <- smart$EVENT[1:500]
y <- survival::Surv(time, event)

fit <- fit_lasso(x, y, nfolds = 5, rule = "lambda.1se", seed = 11)

# Model validation by bootstrap with time-dependent AUC
# Normally boot.times should be set to 200 or more,
# we set it to 3 here only to save example running time.
val.boot <- validate(
  x, time, event,
  model.type = "lasso",
  alpha = 1, lambda = fit$lambda,
  method = "bootstrap", boot.times = 3,
  tauc.type = "UNO", tauc.time = seq(0.25, 2, 0.25) * 365,
  seed = 1010
)
#> Start bootstrap sample 1 
#> Start bootstrap sample 2 
#> Start bootstrap sample 3 

# Model validation by 5-fold cross-validation with time-dependent AUC
val.cv <- validate(
  x, time, event,
  model.type = "lasso",
  alpha = 1, lambda = fit$lambda,
  method = "cv", nfolds = 5,
  tauc.type = "UNO", tauc.time = seq(0.25, 2, 0.25) * 365,
  seed = 1010
)
#> Start fold 1 
#> Start fold 2 
#> Start fold 3 
#> Start fold 4 
#> Start fold 5 

# Model validation by repeated cross-validation with time-dependent AUC
val.repcv <- validate(
  x, time, event,
  model.type = "lasso",
  alpha = 1, lambda = fit$lambda,
  method = "repeated.cv", nfolds = 5, rep.times = 3,
  tauc.type = "UNO", tauc.time = seq(0.25, 2, 0.25) * 365,
  seed = 1010
)
#> Start repeat round 1 fold 1 
#> Start repeat round 1 fold 2 
#> Start repeat round 1 fold 3 
#> Start repeat round 1 fold 4 
#> Start repeat round 1 fold 5 
#> Start repeat round 2 fold 1 
#> Start repeat round 2 fold 2 
#> Start repeat round 2 fold 3 
#> Start repeat round 2 fold 4 
#> Start repeat round 2 fold 5 
#> Start repeat round 3 fold 1 
#> Start repeat round 3 fold 2 
#> Start repeat round 3 fold 3 
#> Start repeat round 3 fold 4 
#> Start repeat round 3 fold 5 

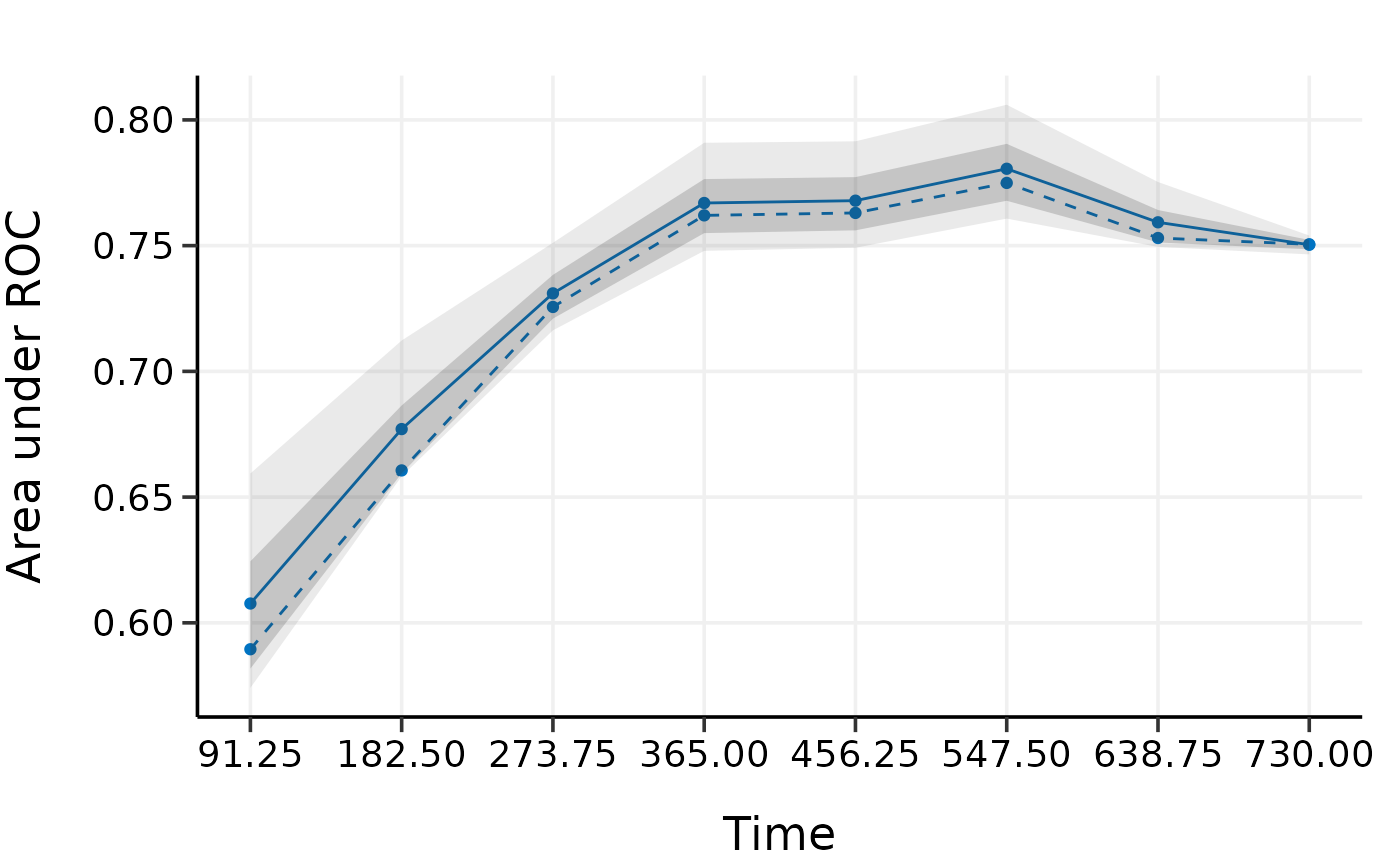
# bootstrap-based discrimination curves has a very narrow band
print(val.boot)
#> High-Dimensional Cox Model Validation Object
#> Random seed: 1010 
#> Validation method: bootstrap
#> Bootstrap samples: 3 
#> Model type: lasso 
#> glmnet model alpha: 1 
#> glmnet model lambda: 0.1182981 
#> glmnet model penalty factor: not specified
#> Time-dependent AUC type: UNO 
#> Evaluation time points for tAUC: 91.25 182.5 273.75 365 456.25 547.5 638.75 730
summary(val.boot)
#> Time-Dependent AUC Summary at Evaluation Time Points
#>              91.25     182.5    273.75       365    456.25     547.5    638.75
#> Mean     0.5853199 0.6249183 0.6686747 0.6930277 0.6939214 0.7019696 0.6952237
#> Min      0.4965657 0.5963733 0.6591369 0.6809984 0.6817096 0.6727704 0.6914517
#> 0.25 Qt. 0.5631313 0.6177748 0.6662872 0.6897655 0.6906126 0.6943256 0.6938939
#> Median   0.6296970 0.6391763 0.6734375 0.6985327 0.6995156 0.7158808 0.6963360
#> 0.75 Qt. 0.6296970 0.6391909 0.6734437 0.6990424 0.7000273 0.7165691 0.6971097
#> Max      0.6296970 0.6392054 0.6734499 0.6995521 0.7005390 0.7172574 0.6978834
#>                730
#> Mean     0.6775340
#> Min      0.6653434
#> 0.25 Qt. 0.6662506
#> Median   0.6671579
#> 0.75 Qt. 0.6836292
#> Max      0.7001006
plot(val.boot)
#>              91.25     182.5    273.75       365    456.25     547.5    638.75
#> Mean     0.5853199 0.6249183 0.6686747 0.6930277 0.6939214 0.7019696 0.6952237
#> Min      0.4965657 0.5963733 0.6591369 0.6809984 0.6817096 0.6727704 0.6914517
#> 0.25 Qt. 0.5631313 0.6177748 0.6662872 0.6897655 0.6906126 0.6943256 0.6938939
#> Median   0.6296970 0.6391763 0.6734375 0.6985327 0.6995156 0.7158808 0.6963360
#> 0.75 Qt. 0.6296970 0.6391909 0.6734437 0.6990424 0.7000273 0.7165691 0.6971097
#> Max      0.6296970 0.6392054 0.6734499 0.6995521 0.7005390 0.7172574 0.6978834
#>                730
#> Mean     0.6775340
#> Min      0.6653434
#> 0.25 Qt. 0.6662506
#> Median   0.6671579
#> 0.75 Qt. 0.6836292
#> Max      0.7001006


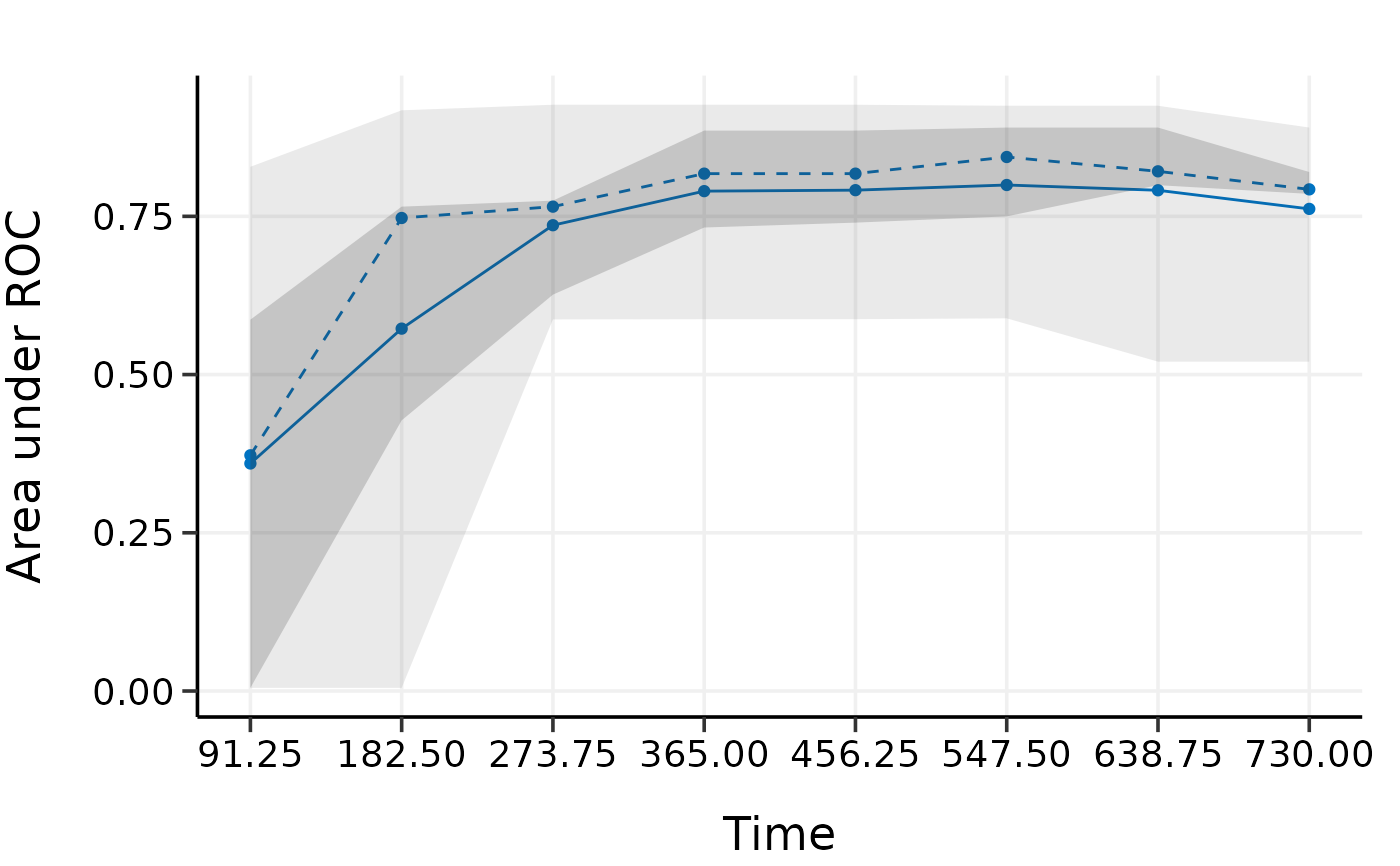
# k-fold cv provides a more strict evaluation than bootstrap
print(val.cv)
#> High-Dimensional Cox Model Validation Object
#> Random seed: 1010 
#> Validation method: k-fold cross-validation
#> Cross-validation folds: 5 
#> Model type: lasso 
#> glmnet model alpha: 1 
#> glmnet model lambda: 0.1182981 
#> glmnet model penalty factor: not specified
#> Time-dependent AUC type: UNO 
#> Evaluation time points for tAUC: 91.25 182.5 273.75 365 456.25 547.5 638.75 730
summary(val.cv)
#> Time-Dependent AUC Summary at Evaluation Time Points
#>              91.25     182.5    273.75       365    456.25     547.5    638.75
#> Mean     0.3871268 0.5553328 0.6603796 0.7094117 0.7108955 0.7166735 0.7087837
#> Min      0.0050000 0.0050000 0.4141414 0.5105351 0.5105351 0.5430566 0.4794722
#> 0.25 Qt. 0.0050000 0.3359944 0.5095475 0.6848001 0.6848001 0.6925183 0.6925183
#> Median   0.2882653 0.7065967 0.7065967 0.7047705 0.7121891 0.6965153 0.7609198
#> 0.75 Qt. 0.7878788 0.8450521 0.8052632 0.8052632 0.8052632 0.8046595 0.8046595
#> Max      0.8494898 0.8840206 0.8663490 0.8416897 0.8416897 0.8466179 0.8063486
#>                730
#> Mean     0.6679114
#> Min      0.4794722
#> 0.25 Qt. 0.6798159
#> Median   0.6826454
#> 0.75 Qt. 0.6925183
#> Max      0.8051053
plot(val.cv)
#>              91.25     182.5    273.75       365    456.25     547.5    638.75
#> Mean     0.3871268 0.5553328 0.6603796 0.7094117 0.7108955 0.7166735 0.7087837
#> Min      0.0050000 0.0050000 0.4141414 0.5105351 0.5105351 0.5430566 0.4794722
#> 0.25 Qt. 0.0050000 0.3359944 0.5095475 0.6848001 0.6848001 0.6925183 0.6925183
#> Median   0.2882653 0.7065967 0.7065967 0.7047705 0.7121891 0.6965153 0.7609198
#> 0.75 Qt. 0.7878788 0.8450521 0.8052632 0.8052632 0.8052632 0.8046595 0.8046595
#> Max      0.8494898 0.8840206 0.8663490 0.8416897 0.8416897 0.8466179 0.8063486
#>                730
#> Mean     0.6679114
#> Min      0.4794722
#> 0.25 Qt. 0.6798159
#> Median   0.6826454
#> 0.75 Qt. 0.6925183
#> Max      0.8051053


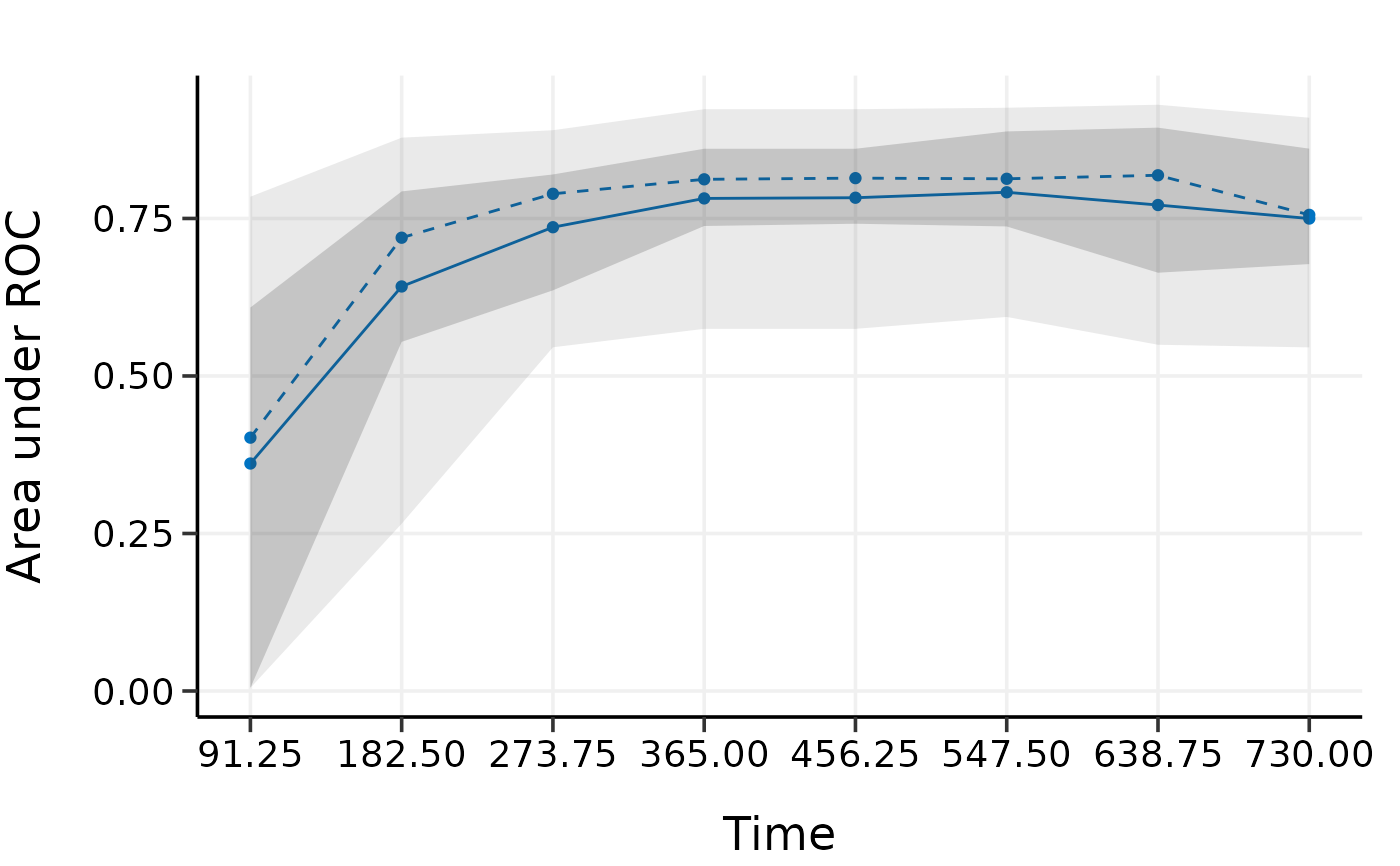
# repeated cv provides similar results as k-fold cv
# but more robust than k-fold cv
print(val.repcv)
#> High-Dimensional Cox Model Validation Object
#> Random seed: 1010 
#> Validation method: repeated cross-validation
#> Cross-validation folds: 5 
#> Cross-validation repeated times: 3 
#> Model type: lasso 
#> glmnet model alpha: 1 
#> glmnet model lambda: 0.1182981 
#> glmnet model penalty factor: not specified
#> Time-dependent AUC type: UNO 
#> Evaluation time points for tAUC: 91.25 182.5 273.75 365 456.25 547.5 638.75 730
summary(val.repcv)
#> Note: for repeated CV, we evaluated quantile statistic tables for
#> each CV repeat, then calculated element-wise mean across all tables.
#> Time-Dependent AUC Summary at Evaluation Time Points
#>                      91.25     182.5    273.75       365    456.25     547.5
#> Mean of Mean     0.3880378 0.6386841 0.6828935 0.7222304 0.7233879 0.7241837
#> Mean of Min      0.0050000 0.3118519 0.4799798 0.5226577 0.5226577 0.5432355
#> Mean of 0.25 Qt. 0.0050000 0.4473707 0.5232730 0.6703547 0.6736697 0.6862773
#> Mean of Median   0.3851895 0.7381908 0.7079172 0.7073084 0.7097813 0.7226275
#> Mean of 0.75 Qt. 0.7214320 0.8020073 0.8153940 0.8266904 0.8266904 0.8012616
#> Mean of Max      0.8235673 0.8940001 0.8879035 0.8841406 0.8841406 0.8675167
#>                     638.75       730
#> Mean of Mean     0.7031466 0.6659973
#> Mean of Min      0.5113682 0.4873410
#> Mean of 0.25 Qt. 0.5973297 0.5873776
#> Mean of Median   0.7440957 0.6617980
#> Mean of 0.75 Qt. 0.7997169 0.7642075
#> Mean of Max      0.8632224 0.8292622
plot(val.repcv)
#>                      91.25     182.5    273.75       365    456.25     547.5
#> Mean of Mean     0.3880378 0.6386841 0.6828935 0.7222304 0.7233879 0.7241837
#> Mean of Min      0.0050000 0.3118519 0.4799798 0.5226577 0.5226577 0.5432355
#> Mean of 0.25 Qt. 0.0050000 0.4473707 0.5232730 0.6703547 0.6736697 0.6862773
#> Mean of Median   0.3851895 0.7381908 0.7079172 0.7073084 0.7097813 0.7226275
#> Mean of 0.75 Qt. 0.7214320 0.8020073 0.8153940 0.8266904 0.8266904 0.8012616
#> Mean of Max      0.8235673 0.8940001 0.8879035 0.8841406 0.8841406 0.8675167
#>                     638.75       730
#> Mean of Mean     0.7031466 0.6659973
#> Mean of Min      0.5113682 0.4873410
#> Mean of 0.25 Qt. 0.5973297 0.5873776
#> Mean of Median   0.7440957 0.6617980
#> Mean of 0.75 Qt. 0.7997169 0.7642075
#> Mean of Max      0.8632224 0.8292622

# # Test fused lasso, SCAD, and Mnet models
#
# data(smart)
# x = as.matrix(smart[, -c(1, 2)])[1:500,]
# time = smart$TEVENT[1:500]
# event = smart$EVENT[1:500]
# y = survival::Surv(time, event)
#
# set.seed(1010)
# val.boot = validate(
#   x, time, event, model.type = "flasso",
#   lambda1 = 5, lambda2 = 2,
#   method = "bootstrap", boot.times = 10,
#   tauc.type = "UNO", tauc.time = seq(0.25, 2, 0.25) * 365,
#   seed = 1010)
#
# val.cv = validate(
#   x, time, event, model.type = "scad",
#   gamma = 3.7, alpha = 1, lambda = 0.05,
#   method = "cv", nfolds = 5,
#   tauc.type = "UNO", tauc.time = seq(0.25, 2, 0.25) * 365,
#   seed = 1010)
#
# val.repcv = validate(
#   x, time, event, model.type = "mnet",
#   gamma = 3, alpha = 0.3, lambda = 0.05,
#   method = "repeated.cv", nfolds = 5, rep.times = 3,
#   tauc.type = "UNO", tauc.time = seq(0.25, 2, 0.25) * 365,
#   seed = 1010)
#
# print(val.boot)
# summary(val.boot)
# plot(val.boot)
#
# print(val.cv)
# summary(val.cv)
# plot(val.cv)
#
# print(val.repcv)
# summary(val.repcv)
# plot(val.repcv)