Compare high-dimensional Cox models by model validation
Source:R/5_1_compare_by_validate.R
compare_by_validate.RdCompare high-dimensional Cox models by model validation
Usage
compare_by_validate(
x,
time,
event,
model.type = c("lasso", "alasso", "flasso", "enet", "aenet", "mcp", "mnet", "scad",
"snet"),
method = c("bootstrap", "cv", "repeated.cv"),
boot.times = NULL,
nfolds = NULL,
rep.times = NULL,
tauc.type = c("CD", "SZ", "UNO"),
tauc.time,
rule = c("lambda.min", "lambda.1se"),
seed = 1001,
trace = TRUE
)Arguments
- x
Matrix of training data used for fitting the model; on which to run the validation.
- time
Survival time. Must be of the same length with the number of rows as
x.- event
Status indicator, normally 0 = alive, 1 = dead. Must be of the same length with the number of rows as
x.- model.type
Model types to compare. Could be at least two of
"lasso","alasso","flasso","enet","aenet","mcp","mnet","scad", or"snet".- method
Validation method. Could be
"bootstrap","cv", or"repeated.cv".- boot.times
Number of repetitions for bootstrap.
- nfolds
Number of folds for cross-validation and repeated cross-validation.
- rep.times
Number of repeated times for repeated cross-validation.
- tauc.type
Type of time-dependent AUC. Including
"CD"proposed by Chambless and Diao (2006).,"SZ"proposed by Song and Zhou (2008).,"UNO"proposed by Uno et al. (2007).- tauc.time
Numeric vector. Time points at which to evaluate the time-dependent AUC.
- rule
Model selection criterion for glmnet models, `"lambda.min"` or `"lambda.1se"`. Defaults to `"lambda.min"`.
- seed
A random seed for cross-validation fold division.
- trace
Logical. Output the validation progress or not. Default is
TRUE.
References
Chambless, L. E. and G. Diao (2006). Estimation of time-dependent area under the ROC curve for long-term risk prediction. Statistics in Medicine 25, 3474–3486.
Song, X. and X.-H. Zhou (2008). A semiparametric approach for the covariate specific ROC curve with survival outcome. Statistica Sinica 18, 947–965.
Uno, H., T. Cai, L. Tian, and L. J. Wei (2007). Evaluating prediction rules for t-year survivors with censored regression models. Journal of the American Statistical Association 102, 527–537.
Examples
data(smart)
x <- as.matrix(smart[, -c(1, 2)])[1:1000, ]
time <- smart$TEVENT[1:1000]
event <- smart$EVENT[1:1000]
# Compare lasso and adaptive lasso by 5-fold cross-validation
cmp.val.cv <- compare_by_validate(
x, time, event,
model.type = c("lasso", "alasso"),
method = "cv", nfolds = 5, tauc.type = "UNO",
tauc.time = seq(0.25, 2, 0.25) * 365, seed = 1001
)
#> Starting model 1 : lasso
#> Start fold 1
#> Start fold 2
#> Start fold 3
#> Start fold 4
#> Start fold 5
#> Starting model 2 : alasso
#> Start fold 1
#> Start fold 2
#> Start fold 3
#> Start fold 4
#> Start fold 5
print(cmp.val.cv)
#> High-Dimensional Cox Model Validation Object
#> Random seed: 1001
#> Validation method: k-fold cross-validation
#> Cross-validation folds: 5
#> Model type: lasso
#> glmnet model alpha: 1
#> glmnet model lambda: 0.01685262
#> glmnet model penalty factor: not specified
#> Time-dependent AUC type: UNO
#> Evaluation time points for tAUC: 91.25 182.5 273.75 365 456.25 547.5 638.75 730
#>
#> High-Dimensional Cox Model Validation Object
#> Random seed: 1001
#> Validation method: k-fold cross-validation
#> Cross-validation folds: 5
#> Model type: alasso
#> glmnet model alpha: 1
#> glmnet model lambda: 0.1086075
#> glmnet model penalty factor: specified
#> Time-dependent AUC type: UNO
#> Evaluation time points for tAUC: 91.25 182.5 273.75 365 456.25 547.5 638.75 730
#>
summary(cmp.val.cv)
#> Model type: lasso
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5512447 0.5892787 0.6118296 0.6703934 0.6522846 0.6827941 0.6663543
#> Min 0.1969697 0.3638949 0.4933239 0.5227411 0.5015440 0.5406118 0.5414032
#> 0.25 Qt. 0.3883162 0.5121101 0.5066906 0.5287065 0.5287065 0.5808059 0.6044632
#> Median 0.6446701 0.5253751 0.5113647 0.6234958 0.6227553 0.6684507 0.6421704
#> 0.75 Qt. 0.7272727 0.6715544 0.6681714 0.8021683 0.7318710 0.7476227 0.6869896
#> Max 0.7989950 0.8734591 0.8795973 0.8748553 0.8765461 0.8764793 0.8567451
#> 730
#> Mean 0.6497359
#> Min 0.5685657
#> 0.25 Qt. 0.6045935
#> Median 0.6472902
#> 0.75 Qt. 0.6660511
#> Max 0.7621791
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5512447 0.5892787 0.6118296 0.6703934 0.6522846 0.6827941 0.6663543
#> Min 0.1969697 0.3638949 0.4933239 0.5227411 0.5015440 0.5406118 0.5414032
#> 0.25 Qt. 0.3883162 0.5121101 0.5066906 0.5287065 0.5287065 0.5808059 0.6044632
#> Median 0.6446701 0.5253751 0.5113647 0.6234958 0.6227553 0.6684507 0.6421704
#> 0.75 Qt. 0.7272727 0.6715544 0.6681714 0.8021683 0.7318710 0.7476227 0.6869896
#> Max 0.7989950 0.8734591 0.8795973 0.8748553 0.8765461 0.8764793 0.8567451
#> 730
#> Mean 0.6497359
#> Min 0.5685657
#> 0.25 Qt. 0.6045935
#> Median 0.6472902
#> 0.75 Qt. 0.6660511
#> Max 0.7621791
#>
#> Model type: alasso
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5507595 0.5930334 0.6119896 0.6708129 0.6531152 0.6855229 0.6689000
#> Min 0.1969697 0.3483014 0.4834263 0.5191235 0.4992296 0.5515548 0.5520277
#> 0.25 Qt. 0.3840206 0.5043381 0.5043835 0.5302921 0.5302921 0.5741340 0.5934681
#> Median 0.6362098 0.5201011 0.5120325 0.6202395 0.6167865 0.6642097 0.6377153
#> 0.75 Qt. 0.7537688 0.7019551 0.6681626 0.8014144 0.7345390 0.7536005 0.6947551
#> Max 0.7828283 0.8904711 0.8919432 0.8829948 0.8847287 0.8841155 0.8665338
#> 730
#> Mean 0.6501607
#> Min 0.5536751
#> 0.25 Qt. 0.5934151
#> Median 0.6453506
#> 0.75 Qt. 0.6715423
#> Max 0.7868205
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5507595 0.5930334 0.6119896 0.6708129 0.6531152 0.6855229 0.6689000
#> Min 0.1969697 0.3483014 0.4834263 0.5191235 0.4992296 0.5515548 0.5520277
#> 0.25 Qt. 0.3840206 0.5043381 0.5043835 0.5302921 0.5302921 0.5741340 0.5934681
#> Median 0.6362098 0.5201011 0.5120325 0.6202395 0.6167865 0.6642097 0.6377153
#> 0.75 Qt. 0.7537688 0.7019551 0.6681626 0.8014144 0.7345390 0.7536005 0.6947551
#> Max 0.7828283 0.8904711 0.8919432 0.8829948 0.8847287 0.8841155 0.8665338
#> 730
#> Mean 0.6501607
#> Min 0.5536751
#> 0.25 Qt. 0.5934151
#> Median 0.6453506
#> 0.75 Qt. 0.6715423
#> Max 0.7868205
#>
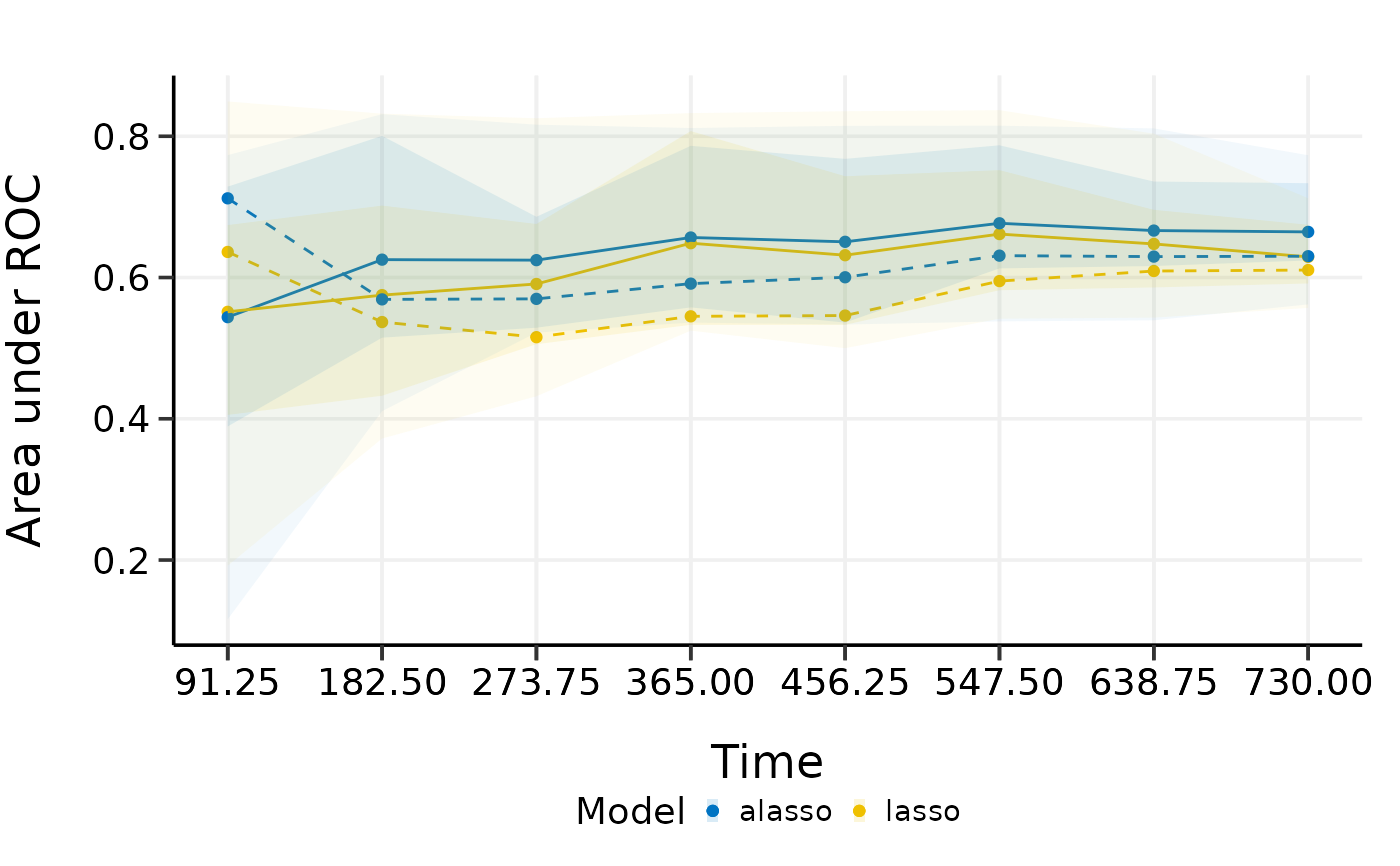
plot(cmp.val.cv)
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5512447 0.5892787 0.6118296 0.6703934 0.6522846 0.6827941 0.6663543
#> Min 0.1969697 0.3638949 0.4933239 0.5227411 0.5015440 0.5406118 0.5414032
#> 0.25 Qt. 0.3883162 0.5121101 0.5066906 0.5287065 0.5287065 0.5808059 0.6044632
#> Median 0.6446701 0.5253751 0.5113647 0.6234958 0.6227553 0.6684507 0.6421704
#> 0.75 Qt. 0.7272727 0.6715544 0.6681714 0.8021683 0.7318710 0.7476227 0.6869896
#> Max 0.7989950 0.8734591 0.8795973 0.8748553 0.8765461 0.8764793 0.8567451
#> 730
#> Mean 0.6497359
#> Min 0.5685657
#> 0.25 Qt. 0.6045935
#> Median 0.6472902
#> 0.75 Qt. 0.6660511
#> Max 0.7621791
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5507595 0.5930334 0.6119896 0.6708129 0.6531152 0.6855229 0.6689000
#> Min 0.1969697 0.3483014 0.4834263 0.5191235 0.4992296 0.5515548 0.5520277
#> 0.25 Qt. 0.3840206 0.5043381 0.5043835 0.5302921 0.5302921 0.5741340 0.5934681
#> Median 0.6362098 0.5201011 0.5120325 0.6202395 0.6167865 0.6642097 0.6377153
#> 0.75 Qt. 0.7537688 0.7019551 0.6681626 0.8014144 0.7345390 0.7536005 0.6947551
#> Max 0.7828283 0.8904711 0.8919432 0.8829948 0.8847287 0.8841155 0.8665338
#> 730
#> Mean 0.6501607
#> Min 0.5536751
#> 0.25 Qt. 0.5934151
#> Median 0.6453506
#> 0.75 Qt. 0.6715423
#> Max 0.7868205
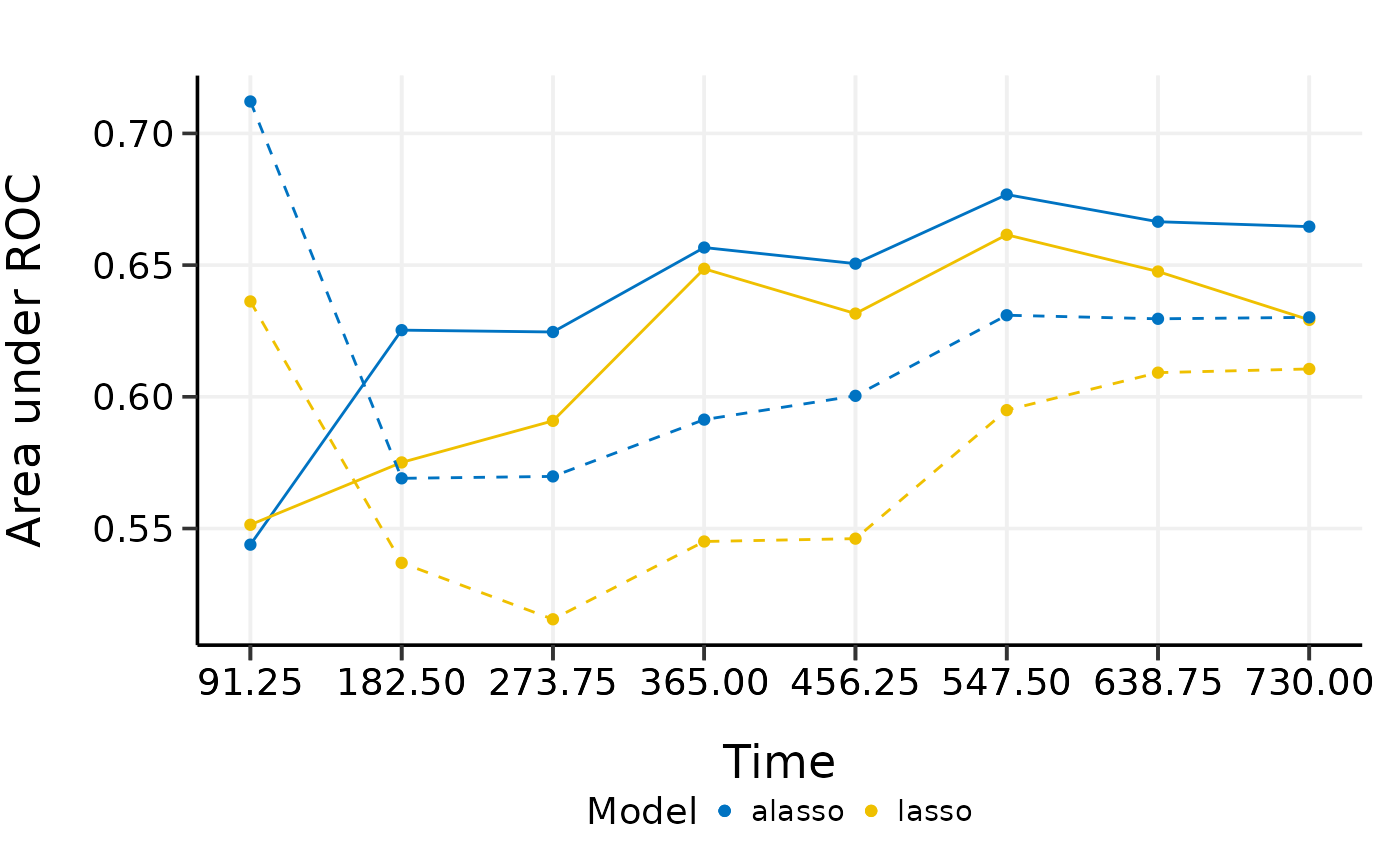 plot(cmp.val.cv, interval = TRUE)
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5512447 0.5892787 0.6118296 0.6703934 0.6522846 0.6827941 0.6663543
#> Min 0.1969697 0.3638949 0.4933239 0.5227411 0.5015440 0.5406118 0.5414032
#> 0.25 Qt. 0.3883162 0.5121101 0.5066906 0.5287065 0.5287065 0.5808059 0.6044632
#> Median 0.6446701 0.5253751 0.5113647 0.6234958 0.6227553 0.6684507 0.6421704
#> 0.75 Qt. 0.7272727 0.6715544 0.6681714 0.8021683 0.7318710 0.7476227 0.6869896
#> Max 0.7989950 0.8734591 0.8795973 0.8748553 0.8765461 0.8764793 0.8567451
#> 730
#> Mean 0.6497359
#> Min 0.5685657
#> 0.25 Qt. 0.6045935
#> Median 0.6472902
#> 0.75 Qt. 0.6660511
#> Max 0.7621791
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5507595 0.5930334 0.6119896 0.6708129 0.6531152 0.6855229 0.6689000
#> Min 0.1969697 0.3483014 0.4834263 0.5191235 0.4992296 0.5515548 0.5520277
#> 0.25 Qt. 0.3840206 0.5043381 0.5043835 0.5302921 0.5302921 0.5741340 0.5934681
#> Median 0.6362098 0.5201011 0.5120325 0.6202395 0.6167865 0.6642097 0.6377153
#> 0.75 Qt. 0.7537688 0.7019551 0.6681626 0.8014144 0.7345390 0.7536005 0.6947551
#> Max 0.7828283 0.8904711 0.8919432 0.8829948 0.8847287 0.8841155 0.8665338
#> 730
#> Mean 0.6501607
#> Min 0.5536751
#> 0.25 Qt. 0.5934151
#> Median 0.6453506
#> 0.75 Qt. 0.6715423
#> Max 0.7868205
plot(cmp.val.cv, interval = TRUE)
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5512447 0.5892787 0.6118296 0.6703934 0.6522846 0.6827941 0.6663543
#> Min 0.1969697 0.3638949 0.4933239 0.5227411 0.5015440 0.5406118 0.5414032
#> 0.25 Qt. 0.3883162 0.5121101 0.5066906 0.5287065 0.5287065 0.5808059 0.6044632
#> Median 0.6446701 0.5253751 0.5113647 0.6234958 0.6227553 0.6684507 0.6421704
#> 0.75 Qt. 0.7272727 0.6715544 0.6681714 0.8021683 0.7318710 0.7476227 0.6869896
#> Max 0.7989950 0.8734591 0.8795973 0.8748553 0.8765461 0.8764793 0.8567451
#> 730
#> Mean 0.6497359
#> Min 0.5685657
#> 0.25 Qt. 0.6045935
#> Median 0.6472902
#> 0.75 Qt. 0.6660511
#> Max 0.7621791
#> 91.25 182.5 273.75 365 456.25 547.5 638.75
#> Mean 0.5507595 0.5930334 0.6119896 0.6708129 0.6531152 0.6855229 0.6689000
#> Min 0.1969697 0.3483014 0.4834263 0.5191235 0.4992296 0.5515548 0.5520277
#> 0.25 Qt. 0.3840206 0.5043381 0.5043835 0.5302921 0.5302921 0.5741340 0.5934681
#> Median 0.6362098 0.5201011 0.5120325 0.6202395 0.6167865 0.6642097 0.6377153
#> 0.75 Qt. 0.7537688 0.7019551 0.6681626 0.8014144 0.7345390 0.7536005 0.6947551
#> Max 0.7828283 0.8904711 0.8919432 0.8829948 0.8847287 0.8841155 0.8665338
#> 730
#> Mean 0.6501607
#> Min 0.5536751
#> 0.25 Qt. 0.5934151
#> Median 0.6453506
#> 0.75 Qt. 0.6715423
#> Max 0.7868205